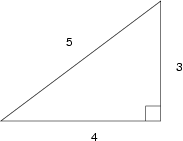
面积6是一个同余数

 
虽然在大学里学过同余，但同余数竟然没听说过（实际上是一样，但数学课本讲的很枯燥）。今天看到了，就顺便了解一下同余数的历史。

公元10世纪，波斯的穆斯林数学家凯拉吉（Al-Karaji）首次提出了“同余数”。不过他是用平方数（
1, 4, 9, 16, 25, 36之类）这个术语进行描述的。他问了这么一个问题：是否存在正整数n，使得
a²-n 和 a²+n都是平方数？如果n存在，那么它便被称为同余数。实际上，希腊数学家丢番图（Diophantus）提出过类似的问题。凯拉吉曾把丢番图的作品翻译到阿拉伯语，因此他提出的这个问题实际上是受丢番图的启发。

1225年，斐波那契（斐波那契数的那位）指出5和7是同余数，但没有给出证明。证明是史上最伟大业余数学家费马在1659年给出的。直到1915年，确定的同余数不到100个。1952年， Kurt Heegner使用了比较高深的数学技巧证明5、13、21、29…..等差数列中的所有质数都是同余数。然而直到1980年，确定的同余数还只是1千个上下。