小时候玩搭积木，弄完以后，要装回盒子里，发现盒子的容量不够，或者重新手动安排一下，或者摇摇盒子得到一点额外的空间。

Nature上最新一期（Vol 460, 13 August 2009），有一篇Torquato and Jiao写的文章，讨论怎么在一定空间内寻找堆积的最高密度。使用的单元包括普拉图和阿基米德提出的结构单元（四面体、六面体、八面体、十二面体…，如下图所示）。之前，人们关注的比较多的是，球体的随机致密排布（Random Close Packing）。对于这些类似积木的单元，则由于问题更复杂而研究得比较少。在三维空间里，球体由于对称性，只有平移的三个自由度，而列出的结构单元则增加了转动的三个自由度。在现在这篇文章里，提到的是一种“适应收缩单元”（adaptive shrinking cell）的优化方法，利用计算机蒙特卡罗方法进行模拟，去逼近和得到理论的相对密度上限。

但是，实际问题里的堆积，往往无法达到理论上限，其中一个原因就是摩擦力的影响形成拥塞结构，而无法进一步致密。除非施加外力或者改变温度来打破形成的拥塞结构（Liu and Nagel, 1998）。

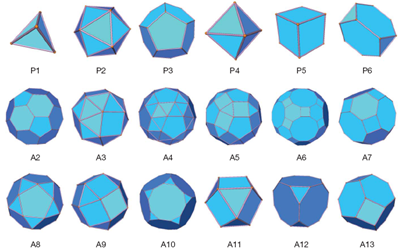
这个工作不是针对解决实际问题的，比较有趣。我这里就简称为“搭积木”问题了。由于最近的工作，有一个类似的问题，就是研究球体随机排布的，寻找一个计算机模拟的拓扑结构，来看非均质材料的宏观性能。不过这个问题已经在上世纪80年代，被一批物理学家做完了。现在就是拿来做做工程应用。Torquato还有一本书关于非均质材料细观力学的，Random Heterogeneous Materials: Microstructure and Macroscopic Properties, Springer (2001).

[1] Torquato and Jiao, Dense Packings of the Platonic and Archimedean solids. Nature Vol 460, 13 August 2009.
[2] Liu and Nagel, Nonlinear dynamics: Jamming is not just cool any more. Nature Vol 396, 05 November 1998.

原文PDF