上周三出现在莫斯科上空的“UFO”云

小时候玩搭积木，弄完以后，要装回盒子里，发现盒子的容量不够，或者重新手动安排一下，或者摇摇盒子得到一点额外的空间。

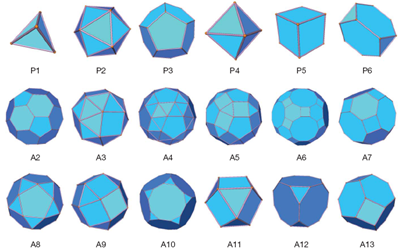
Nature上最新一期（Vol 460, 13 August 2009），有一篇Torquato and Jiao写的文章，讨论怎么在一定空间内寻找堆积的最高密度。使用的单元包括普拉图和阿基米德提出的结构单元（四面体、六面体、八面体、十二面体…，如下图所示）。之前，人们关注的比较多的是，球体的随机致密排布（Random Close Packing）。对于这些类似积木的单元，则由于问题更复杂而研究得比较少。在三维空间里，球体由于对称性，只有平移的三个自由度，而列出的结构单元则增加了转动的三个自由度。在现在这篇文章里，提到的是一种“适应收缩单元”（adaptive shrinking cell）的优化方法，利用计算机蒙特卡罗方法进行模拟，去逼近和得到理论的相对密度上限。

但是，实际问题里的堆积，往往无法达到理论上限，其中一个原因就是摩擦力的影响形成拥塞结构，而无法进一步致密。除非施加外力或者改变温度来打破形成的拥塞结构（Liu and Nagel, 1998）。

(维基百科)

谁偷吃了一块？

这篇文章是几天前写的《分蛋糕是极其复杂的》的扩充，最近实在没空码太多字，本文也只是寥寥而作。
在数学社会学，尤其是博弈论中，Envy-free（翻译过来大概就是“没有嫉妒”或“心满意足”？）是专门指如何给N位满腹心事各怀鬼胎的人分东西，比如蛋糕、糖果，如何让每个人都感到心满意足。大概我们这些从小受孔融让梨（人家是成功人士，虽被“恶人”曹操杀了，但好歹是励志故事），尊老爱幼教育的人不以为然，但每当看到别人拿走自己眼里的“大块”蛋糕（或肉、鱼、鸡腿），是否心理会隐隐感到不快，也就是嫉妒？然后说不定还藏在心底，该天再报复一下：-）很多时候公平是能让问题消于无形。


分蛋糕或公平分配问题最早是Steinhaus于1948年提出的，1980 年费城Swarthmore学院的Walter Stromquist证明存在一个Envy-free解。换句话说，一块蛋糕切N-1次分给N个人，让每个人都满意是可能的。N=2和N=3的情况比较简单（其实N=3已经相当繁琐了），1992年Steven Brams和Alan Taylor证明了N>3的情况，但算法过于复杂，他们为此特地写了一本书来剖析如何公平的分蛋糕。最近香港城市大学的Xiaotie Deng和同事提出了一种更高效分蛋糕算法，算法的计算可在多项式时间内完成。但唯一令人遗憾的问题是算法适用范围是N=3，另外的一些特例只能得到近似的Envy-free解。

10幅罗夏克墨迹测验图片

墨迹测验又称为罗夏克墨渍测验是人格测验的投射技术之一，由瑞士精神医生罗夏克(Rorschach)于1921年最先编制。测验由10张有墨渍的卡片组成，其中 5张是白底黑墨水，2张是白底及黑色或红色的墨水，另外3张则是彩色的。受试者会被要求回答他们最初为卡片看起来像什么及后来觉得像什么。心理学家再根据他们的回答及统计数据判断受试者的性格。一些研究人员认为墨迹测验是伪科学。